Doğal sayılar, $mathbb{N} = { 0, 1, 2, 3, 4, 5, 6, 7, ... }$ şeklinde sıralanan tam sayılardır. Negatif değer almazlar. Bazı kaynaklarda "0" doğal sayı olarak alınmaz. Matematikte hala sıfırın bir doğal sayı alınıp alınmayacağı tartışma konusudur, ancak eğer cebirsel inşâlar yapılmak isteniyorsa "0" sayısının doğal sayı olarak alınması avantaj sağlayabilir. Matematiğin diğer dallarında da problem hangi durumda daha kolay ifade edilebilecekse doğal sayılar kümesi de o şekilde alınır.

Konu başlıkları

[gizle]

Sayı değeri [değiştir]

Bir doğal sayının rakamlarının belirttiği değere rakamların sayı değeri denir. Doğal sayının rakamlarının toplamına rakamların sayı değerleri toplamı denir.

Basamak değeri [değiştir]

9 basamaklı bir doğal sayının basamaklarının

Birler basamağının basamak değeri :1
Onlar basamağının basamak değeri :10
Yüzler basamağının basamak değeri :100
Binler basamağının basamak değeri :1.000
On binler basamağının basamak değeri :10.000
Yüz binler basamağının basamak değeri :100.000
Milyonlar basamağının basamak değeri :1.000.000
On milyonlar basamağının basamak değeri :10.000.000
Yüz milyonlar basamağının basamak değeri :100.000.000

Onlu sayma düzeninde bir basamağın değeri sağındaki basamağın 10 katıdır.

Bir rakamın basamak değeri o rakam ile rakamın yazıldığı basamağın çarpımıyla bulunur..

12345 sayısındaki 2 nin basamak değeri 2 (sayı değeri) ve 1000 (basamak değeri) çarpılarak 2 X 1000 2000 şeklinde bulunur.

Peano Belitleri tanımı [değiştir]

peano belitleri tarihsel olarak doğal sayıların en genel (ve sezgisel) tanımıdır. Modern tanımlar bu tanımı sağlar.

Sıfır bir doğal sayıdır.
Her doğal sayının, yine bir doğal sayı olan bir ardılı vardır.
Ardılı sıfır olan hiç bir doğal sayı yoktur.
Ardılları eşit olan doğal sayılar da birbirine eşittir.
Doğal sayılardan oluşan bir küme, sıfırı ve her doğal sayının ardılını içeriyorsa o küme doğal sayılar kümesine eşittir.

Sıfırı doğal sayı olarak kabul etmeyen grup, buradaki belitlerin "Bir, bir doğal sayıdır." olarak kabul eder.

ZFC tanımı [değiştir]

Zermelo-Freankel küme kuramı doğal sayılar, von Neumann sıral sayılarıyla inşa edilebilir. Buna göre her sayı temelde bir kümedir. Eğer sıfır boşküme olarak tanımlanırsa ve her n sayının ardılı, $n +$ , n $cup$ {n} olarak verilirse, doğal sayılar inşa edilmiş olur.

$0=emptyset$

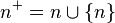
$n^+ = n cup { n }$

Bu tanım doğal sayıların yinelgen bir yapıda olduğunu da belirtmiş olur. Bu yinelgen tanımla sayılar,

0={}

1={0}

2={0,1}

3={0,1,2}

...

n+1={0,1,...,n}

Bu tanımda iki doğal sayının eşitliği sayıların öğe sayısına dayanır.

Russell'ın farklı bir tanımı daha genel görünebilir:0 DOĞAL SAYIDIR

$0={emptyset}$ (sıfır, hiç öğesi olmayan tüm kümelerin kümesi)

$n^+ = { x cup { y } , | , x in n , text{ve} , y notin x }$ (n nin ardılı, öğe sayısı n olan tüm kümelerin kümesi)

Ne var ki bu tanım belitsel küme kuramlarında geçerli değildir, çünkü bir sayı, küme olamayacak kadar büyük topluluklar olmak zorunda kalıyor. Ancak tipler kuramı gibi kuramlarda geçerlidir.

Büyüklük ve küçüklük ilişkileri [değiştir]

Doğal sayıların sıralanmasına en büyük basamaktan başlanır. Aynı basamakta büyük rakam bulunan sayı diğerinden büyüktür.

İki sayının yüz milyonlar basamaklarında eşit rakamlar bulunuyor. Bu nedenle karşılaştırma bir sonraki basamak olan on milyonlar basamaklarında yapılır. Bu basamaklarda 9 > 8 olduğundan 894.125.067 > 887.954.700 yazılır. “ 894.125.067 büyüktür 887.954.700 şeklinde okunur.”

$mathbb{N} = { 0, 1, 2, 3, 4, 5, 6, 7, ... }$ Doğal Sayılar Kümesinde; iki doğal sayının toplamı yine bir doğal sayı olur.

[değiştir] Doğal sayılarda işlemler

Doğal sayılar toplama ve çarpma işlemine göre kapalıdırlar. İki doğal sayının çarpımı veya toplamı yine bir doğal sayıdır. Örneğin : 3.5=15 , 7.9=63 İki doğal sayının farkı veya bölümü bir doğal sayı olmayabilir bu nedenle doğal sayılar çıkarma ve bölme işlemine göre kapalı değildir. Örn: 9-12 = -3 , 2/4 = 1/2 gibi.

Toplama işlemi [değiştir]

Toplama işlemi ileri doğru sayma işlemidir. Toplama işlemine katılan sayılara terim, işlemin sonucuna toplam denir. Toplama işlemi sayıların aynı basamakları arasında yapılır. Bu nedenle toplama işleminde sayılar aynı basamaklar alt alta gelecek şekilde yapılır.

Doğal sayılarda toplama aşağıdaki cebirsel kurallara uyar:

Toplamsal birim öğe:

a + 0 = a

Toplamanın değişme özelliği:

a + b = b + a

Toplamanın birleşme özelliği:

(a + b) + c = a + (b + c)

Toplamanın çarpma üzerine dağılma özelliği (sağdan dağılma):

(a + b)c = ac + bc

Bir a sayısını bir b sayısıyla toplamak, a sayısının b kere ardılını almak olarak tanımlanır. Daha matematiksel bir tanım verilmek istenirse $A r d (n)$ gösterimi n sayısının ardılını ifâde etmek üzere, toplama aşağıdaki belitlerle tanımlanır:

$a + 0 = a$
$a + A r d (b) = A r d (a + b)$

Bu belitlerden yola çıkarak ardıllık işlemini toplama cinsinden göstermek mümkündür: 2. belitte b=0 seçilirse

a + A r d (0) = a r d (a + 0)

sıfırın adrılı birdir, o halde,

A r d (a) = a + 1

olduğu kolaylıkla görülür.

Çarpma işlemi [değiştir]

Çarpma işlemi ard arda toplama işlemidir. Çarpma işlemine katılan sayılara çarpan, işlemin sonucuna çarpım denir.

Doğal sayılarda çarpma aşağıdaki cebirsel kurallara uyar:

Çarpımsal birim öğe:

a1 = a

Çarpmanın değişme özelliği:

ab = ba

Çarpmanın birleşme özelliği:

(ab)c = a(bc)

Çarpmanın toplama üzerine dağılma özelliği (soldan dağılma):

c(a + b) = ca + cb

Bir a sayısını bir b sayısıyla çarpmak, a sayısının b kere toplamını almak olarak tanımlanır. Daha matematiksel bir tanım verilmek istenirse $A r d (n)$ gösterimi n sayısının ardılını ifâde etmek üzere, çarpma aşağıdaki belitlerle tanımlanır:

$a 1 = a$
$a , Ard(b) = ab + a$ DOĞAL SAYILAR

0, 1, 2, 3, ... , 50, ... devam eden sayılara doğal sayılar denir.
Doğal sayılar kümesi D ile gösterilir.
D = {0, 1, 2, 3, 4, 5, ... }
İkinin katı olan sayılara çift doğal sayılar, çift doğal sayılardan bir sonra gelen sayılara da tek doğal sayılar denir.
n bir doğal sayı iken;
Çift doğal sayılar : 2
Tek doğal sayılar : 2 + 1 biçiminde gösterilir.
Sayma Sayıları
Sıfır dışındaki doğal sayılara sayma sayıları denir.
S = {1, 2, 3, 4, 5, ...}

SAYI DOĞRUSU

Doğal sayılar kümesinin elemanları sırası bozulmadan, bir doğrunun eşit aralıklardaki bazı noktaları ile bire-bir eşlenirse bu doğruya sayı doğrusu denir.[SIZE=4]

ONLUK SAYMA DÜZENİ

Sayı sistemimiz onluk sayma düzenine göredir. Bu düzende çokluklar birlik, onluk, yüzlük, binlik gibi gruplara ayrılır. Bir doğal sayıda bu grupların yerleri bellidir. Örneğin, 2543 sayısı içinde 3 birlik, 4 onluk, 5 yüzlük, 2 binlik vardır.

RAKAM

Ona kadar olan doğal sayıları gösteren işaretlere rakam denir.
Rakamlar kümesi : R = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} olarak tanımlanır.
Onluk sistemde on tane rakam kullanılır.

BASAMAK DEĞERİ

Rakamların sayı içinde bulundukları basamağa göre aldıkları değerlere basamak değeri ya da bağıl değer denir.
Bir sayının rakamlarının basamak değerleri toplamı sayının kendisini verir.

SAYI DEĞERİ

Rakamların sayı içindeki basamak değerleri gözönüne alınmadan tek başına gösterdiği değere sayı değeri ya da mutlak değeri denir.

ÇÖZÜMLEME

Bir sayının içinde kaç tane birlik, kaç tane onluk, kaç tane yüzlük, kaç tane binlik, ... varsa bunları ayırarak toplam biçiminde yazmaya çözümleme denir.

2345 = 1000 + 1000 + 100 + 100 + 100 +
10 + 10 + 10 + 10 + 1 + 1 + 1 + 1 + 1

GRUPLAMA

Sayıları basamak değerlerinin toplamı biçimde yazmaya gruplama denir.

2345 = 2000 + 300 + 40 + 5 veya
= 2 binlik + 3 yüzlük + 4 onluk + 5 birlik

SAYILARIN ÜSLÜ BİÇİMDE GÖSTERİLMESİ

ÜSLÜ SAYILARIN OKUNUŞU

4 4 üssü 2 (4'ün karesi, 4'ün ikinci kuvveti)
5 5 üssü 3 (5'in kübü, 5'in üçüncü kuvveti)
3 3 üssü 4 (3'ün dördüncü kuvveti)

ÜSSÜN ANLAMI

Üs tabanın kendisi ile kaç kez çarpılacağını gösterir.

10 = 10 x 10 = 100
5 = 5 x 5 x 5 = 125
4 = 4 x 4 x 4 x 4 = 256
3 = 3 x 3 x 3 x 3 x 3 = 243
2 = 2 x 2 x 2 x 2 x 2 x 2 = 64

ÜSLÜ SAYILARIN ÖZELLİKLERİ

Bir sayıda üs yazılmamışsa üs 1 dir. 3=3, 7=7, 10=10, 15=15
Üssü 0 olan sayı 1'e eşittir. 80=1, 9=1, 160=1, 0=1Kaynakwh:
Üssü 1 olan sayı kendisine eşittir. 7=7, 1000=1000, 64=64, 1=1
1 sayısının bütün kuvvetleri 1'e eşittir. 1=1, 1=1, 1=1
Tabanları aynı olan üslü sayılar çarpılırken; ortak taban yazılır, üsler toplanıp bir tek üs olarak yazılır.

ÜSLÜ BİÇİMDE ÇÖZÜMLEME

Bir sayı üslü biçimde çözümlenirken basamak değeri 10'un üssü şeklinde yazılır.

5679 = (5 x 1000) + (6 x 100) + (7 x 10) + (9 x 1)
=(5 x 10) + (6 x 10) + (7 x 10) + (9 x 1)

DOĞAL SAYILARDA SIRALAMA

Sayı doğrusu üzerindeki her doğal sayı sağındaki sayıdan küçük solundaki sayıdan büyüktür. Doğal sayılar sıralanırken aralarına küçük ( < ) veya büyük ( > ) işareti konur.

Küçük < Büyük
Büyük > Küçük

< işaretinin sivri ucuyla gösterdiği sayı diğer taraftaki sayıdan küçüktür.

DÖRT İŞLEM

DOĞAL SAYILARDA TOPLAMA

AB = olmak üzere, (AB) kümesinin eleman sayısına toplama denir.
A={1,2} ve B={3, 4, 5} ise
s(A) + s(B) = s(AB) = 2 + 4 = 6
Toplama işleminde toplanan sayıların herbirine terim denir. İşlemin sonucuna da toplam denir.
Toplama işlemi, ileriye doğru saymanın kısa yoldan yapılışıdır. Aynı türden ve birimleri aynı olan çokluklar toplanabilir.

TOPLAMA İŞLEMİNİN ÖZELLİKLERİ

KAPALILIK ÖZELLİĞİ

İki doğal sayının toplamı yine bir doğal sayıdır. Buna kapalılık özelliği denir.

3D, 4D için 3 + 4 = 7D dir.
9D, 13D için 9 + 13 = 22D dir.
aD, bD için (a + b)D dir.

DEĞİŞME ÖZELLİĞİ

Toplama işleminde terimlerin yerleri değiştirilirse toplam değişmez. Buna toplamada değişme özelliği denir.
3 + 5 = 8 = 5 + 3
aD, bD ise; a + b=b + a dir.

BİRLEŞME ÖZELLİĞİ

Toplama işleminde terimler ikişer ikişer gruplandırırsa toplam değişmez. Bu özelliğe
toplama işleminin birleşme özelliği denir.

3 + (4 + 6) = (3 + 4) + 6 3 + 10 = 7 + 6 13 = 13
aD, bD, cD ise (a + b) + c = a + (b + c) dir.

Çok terimli toplama işlemlerinde terimler kendi aralarında gruplandırılarak işlem kolaylığı sağlanır.

ETKİSİZ (BİRİM) ELEMAN

Sıfır ile bir doğal sayının toplamı o doğal sayıya eşittir.

5 + 0 = 5
0 + 6 = 6

Doğal sayılar kümesinde toplama işleminin etkisiz elemanı 0'dır.
Kaynakwh:
DOĞAL SAYILARDA ÇIKARMA

A = {a,b,c,d,e} B = {d,e}
s(A) = 5 ve s(B) = 2 dir.
s(A) - s(B) = s(C)
5 - 2 = 3 olarak gösterilir. Burada 5 : eksilen; 2 : çıkan 3 : fark olarak adlandırılır.

B A ise A - B kümesinin eleman sayısına A ve B kümelerinin eleman sayılarının farkı denir. Bu farkı bulmak için yapılan işleme çıkarma işlemi adı verilir.

Çıkarma geriye doğru saymanın kısa yapılışıdır. Sağlaması; a-b=c ise a=b + c olacak şekilde yapılır. Çıkarma işlemi toplamanın tersidir.

ÇIKARMA İŞLEMİNİN ÖZELLİKLERİ

Kapalılık özelliği yoktur. 5D ve 6D için; 5-6 doğal sayı değildir.
Değişme özelliği yoktur. 6D ve 2D için; 6-2=4D; 2-6 doğal sayı değildir.
Birleşme özelliği yoktur. 7-(5-2) (7-5)-2 7-3 2-2 4 0
Doğal sayılar kümesinde çıkarma işlemine göre etkisiz (birim) eleman yoktur. 3-0=3 olmakla beraber 0-3 3'tür.

DOĞAL SAYILARDA ÇARPMA

Elemanlarının sayısı bilinen A ve B kümeleri için s(A)=a, s(B)=b ve s(A ) x s( B)=m ise, m doğal sayısına a ile b'nin çarpımı denir. m=a x b biçiminde gösterilir. Çarpma işareti ( x ) ya da( . )' dır.

ÇARPMA İŞLEMİNİN ÖZELLİKLERİ

KAPALILIK ÖZELLİĞİ

İki doğal sayının çarpımı yine bir doğal sayıdır. Bu özelliğe doğal sayılar kümesi çarpma işlemine göre kapalıdır denir.

DEĞİŞME ÖZELLİĞİ

Bir çarpma işleminde çarpanların yerleri değiştirilirse çarpım değişmez. Bu duruma çarpmanın değişme özelliği denir.

4 x 5 = 20 5 x 4 = 20 4 x 5 = 5 x 4'tür.
aD, bD için; a x b = b x a 'dır.

BİRLEŞME ÖZELLİĞİ

Çarpma işleminde terimler ikişer ikişer gruplandırılarak çarpılırsa çarpım değişmez. Bu özelliğe çarpma işleminin birleşme özelliği denir.

4D, 5D, 2D için
4 x (5 x 2) = (4 x 5) x 2 4 x 10=20 x 2; 40=40'tır.

ETKİSİZ (BİRİM) ELEMAN

Bir sayının 1 ile çarpımı kendisine eşittir. 1 sayısı çarpma işlemini etkilemez. 1 sayısına çarpma işleminin etkisiz (birim) elemanı denir.

1 x 5=5 5 x 1=5 5 x 1=1 x 5=5'dir.
aD için a x 1=1 x a=a 'dır.

YUTAN ELEMAN

Bir sayının sıfır ile çarpımı sıfıra eşittir. Bu nedenle 0 sayısına çarpma işleminde yutan eleman denir.

4 x 0=0 0 x 4=0 4 x 0=0 x 4=0 'dır.
aD için 0 x a=a x 0=0 'dır.

ÇARPMANIN TOPLAMA VE ÇIKARMA ÜZERİNE DAĞILMA ÖZELLİĞİ

aD, bD, cD için a x (b + c)=(a x b) + (a x c) ve
aD, bD, cD için a x (b-c)=(a x b) - (a x c) 'dir.
Bu özelliğe, çarpmanın toplama ya da çıkarma üzerine dağılma özelliği denir.

ÇARPMADA KOLAYLIKLAR

Bir sayıyı 10, 100, 1000, ... ile çarpmak için, sayının sağına bir, iki, üç, ... sıfır yazılır.

14 x 10 = 140
16 x 100 = 1600
22 x 1000 = 22000
7 x 10000 = 70000
Bir sayıyı 25 ile çarpmak için, sayı 100 ile çarpılır. Çarpım 4'e bölünür.

25 x 36=(36 x 100)/4=900

Bir sayı 50 ile çarpılırken, sayı 100'le çarpılır, çarpım 2'ye bölünür.

78 x 50=(78 x 100)/2=7800/2=3200

Bir sayı 5'le çarpılırken, sayı 10'la çarpılır sonra 2'ye bölünür.

89 x 5=(89 x 10)/2=890/2=445

Bir sayı 9'la çarpılırken, sayı 10'la çarpılır, çarpımdan sayının kendisi çıkarılır.

56 x 9=(56 x 10)-56, 560-56=504

DOĞAL SAYILARDA BÖLME

aD, bD ve b0 olmak üzere, a x b=c olarak şekilde bir c doğal sayısı varsa, c sayısına a'nın b'ye bölümü denir. a/b=c veya a:b=c olarak gösterilir.

BÖLMENİN SAĞLAMASI

Sağlama işlemi, Bölünen = (bölen x bölüm) + kalan eşitliğiyle yapılır.

Çarpma ve bölme işlemleri birbirinin tersidir.

BÖLME İŞLEMİNİN ÖZELLİKLERİ

Bölme işleminin doğal sayılarda kapalılık özelliği yoktur.

4D, 3D için 4/3=doğal sayı değildir.

Bölme işleminin doğal sayılarda değişme özelliği yoktur.

5D, 15D için, 15/5 5/15

Doğal sayılarda bölme işleminin birleşme özelliği yoktur.

(24/4)/2 24/(4/2) 6/2 24/2 3 12

Doğal sayılar kümesinde bölme işleminin etkisiz elemanı yoktur.

2/1 1/2 2 0,5

Bir doğal sayının 1'e bölümü kendisine eşittir.

aD için a/1=a dır. 1/1=1, 39/1=39, 3/1=3, 101/1=101

Sıfırın (0) bir sayma sayısına bölümü sıfırdır.

0/a=0 'dır. 0/4=0, 0/100=0, 0/15=0

0 hariç, bir doğal sayının kendisine bölümü 1'e eşittir.

aD için a/a=1 'dir. 6/6=1, 109/109=1, 10/10=1, 88/88=1

Bir doğal sayı sıfıra bölünemez.

5/0=tanımsız, 12/0=tanımsız

Bir sayıyı 10, 100, 1000 ... ile bölmek;

10'a bölerken bir sıfır silinir. 400/10 = 40
100'e bölerken iki sıfır silinir. 200/100 = 2
1000'e bölerken üç sıfır silinir. 3000/1000 = 3